很多人在接触卷积神经网络之前就接触过卷积运算,比如信号与系统的连续信号卷积和离散信号卷积。本文将我的理解出发对比卷积神经网络的卷积和我们信号卷积的区别与联系。介绍卷积神经网络中的卷积操作,以及不同的卷积策略。为后续深入高效小网络及模型压缩相关概念和原理做准备。
信号卷积
卷积表征函数f与经过翻转和平移的g的乘积函数所围成的曲边梯形的面积。信号与系统中,采样信号经过系统响应得到系统输出。一维卷积的数学表达: \[
离散卷积:z[n]=(x * y)[n] = \sum_{m = -\infty}^{+\infty}x[m]\cdot y[n - m]\\连续卷积: y(x)=(f * h)(t) = \int_{-\infty}^{+\infty}f(\tau)\cdot h(t - \tau)\mathop{}\!\mathrm{d}\tau
\] 我们采集到的信号通常是离散的,因此,后续讲解的就是离散卷积。看下维基百科的卷积可视化。 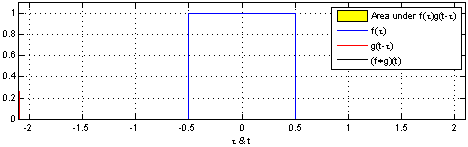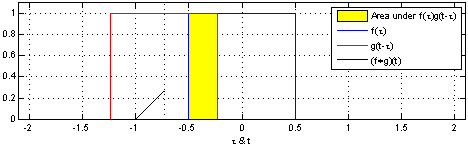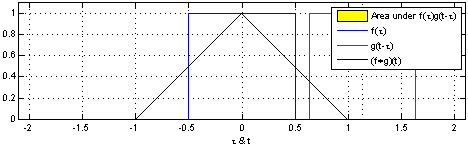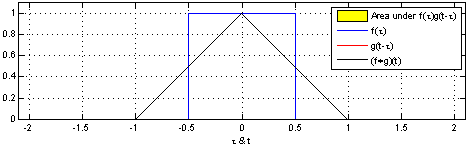
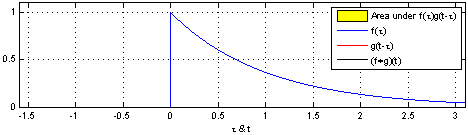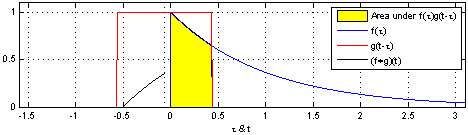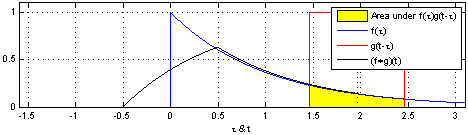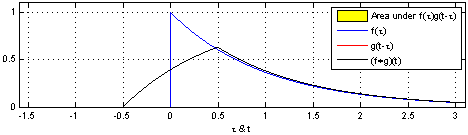
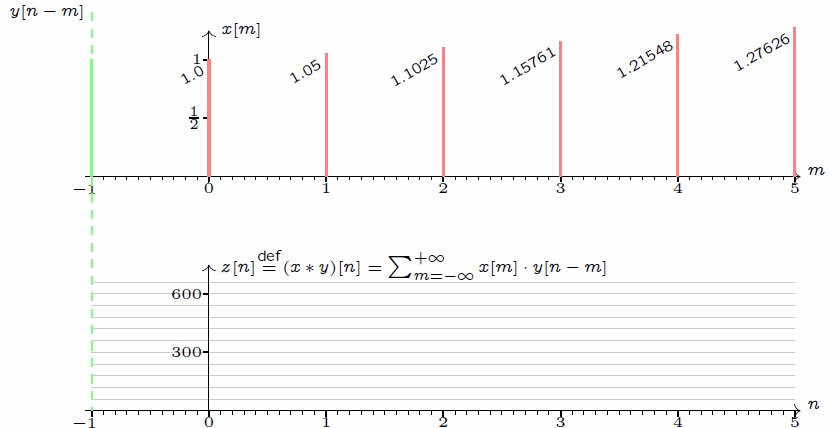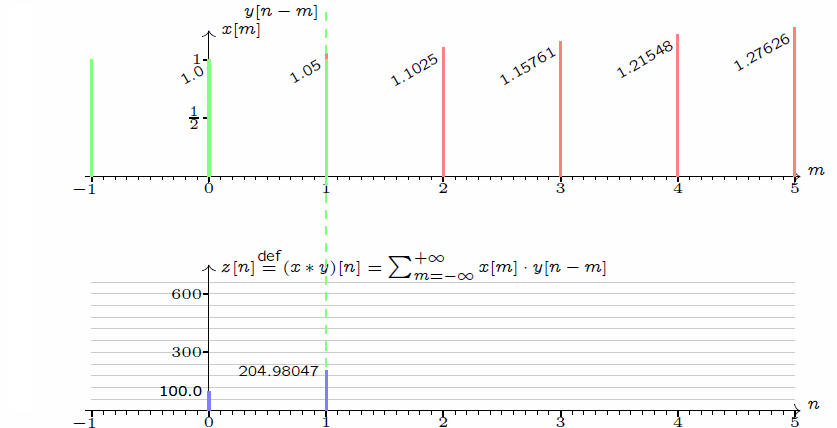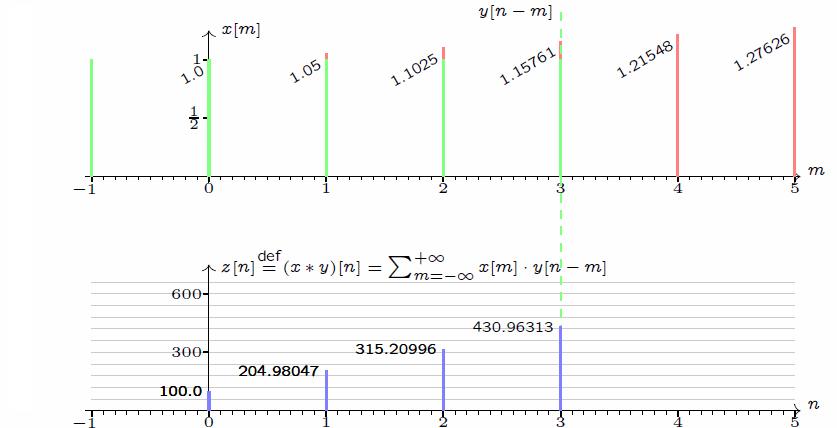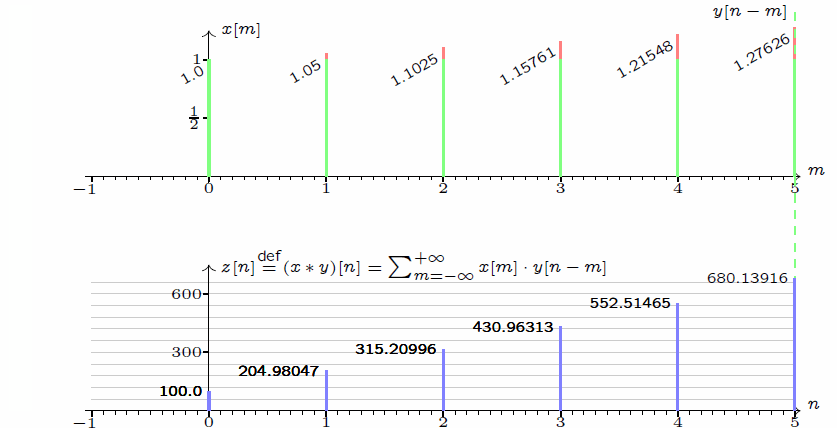
一维离散卷积比较好理解,每个输出元素都是卷积核(系统响应)和信号的局部乘积的和。卷积操作是一种滤波操作,信号与系统的高通滤波,低通滤波等,因此,通过卷积操作可以获得某个方面属性的增强。一维离散卷积通常是在时域卷积,图像,激光雷达回波等属于空间属性。
CNN的卷积
卷积计算
以图像为例。图像卷积即二维离散卷积,图像的矩阵表示为\(h*w\),元素数值大小为无符号整型通常在[0,255]之间。二维离散卷积的公式定义: \[ S[i, j] = (F ∗ K)(i, j) = \sum_m\sum_n F(m, n)K(i − m, j − n) \] 卷积是可交换的(commutative),该公式可转变为: \[ S[i, j] = (F ∗ K)(i, j) = \sum_m\sum_n F(i-m, i-n)K( m, n),K即我们常说的卷积核 \]
图像卷积示例:
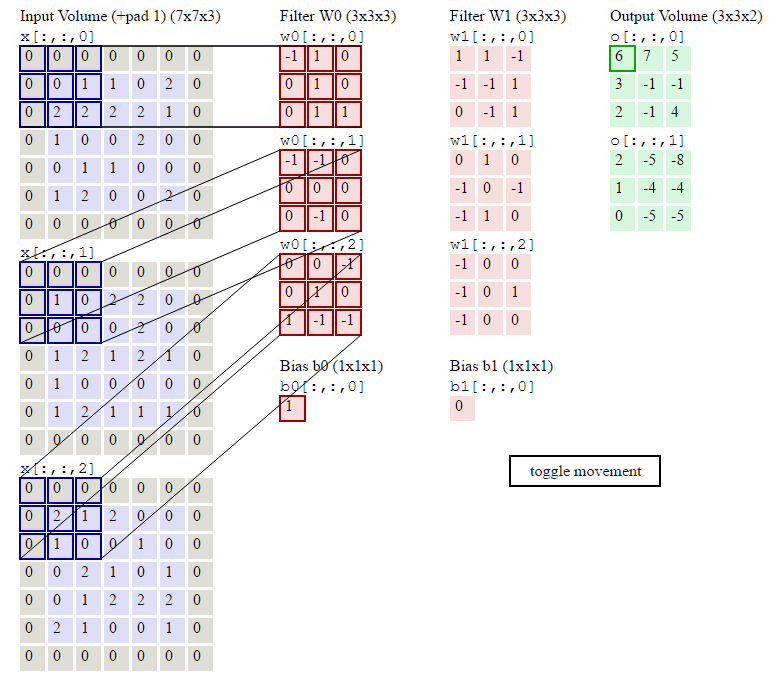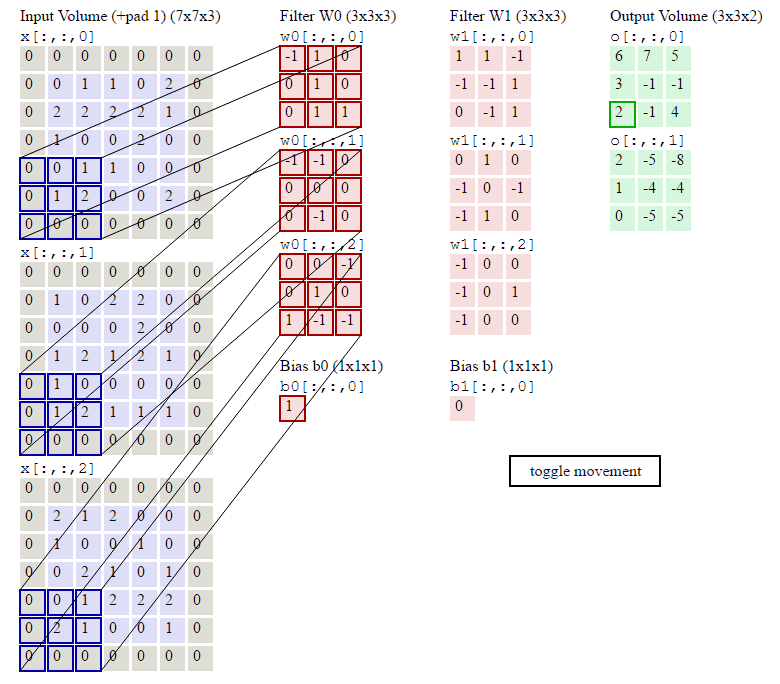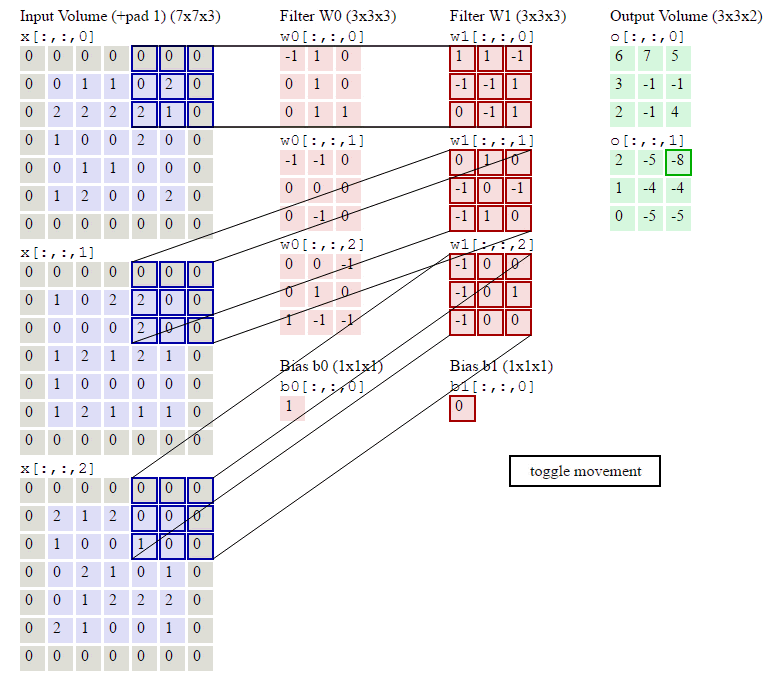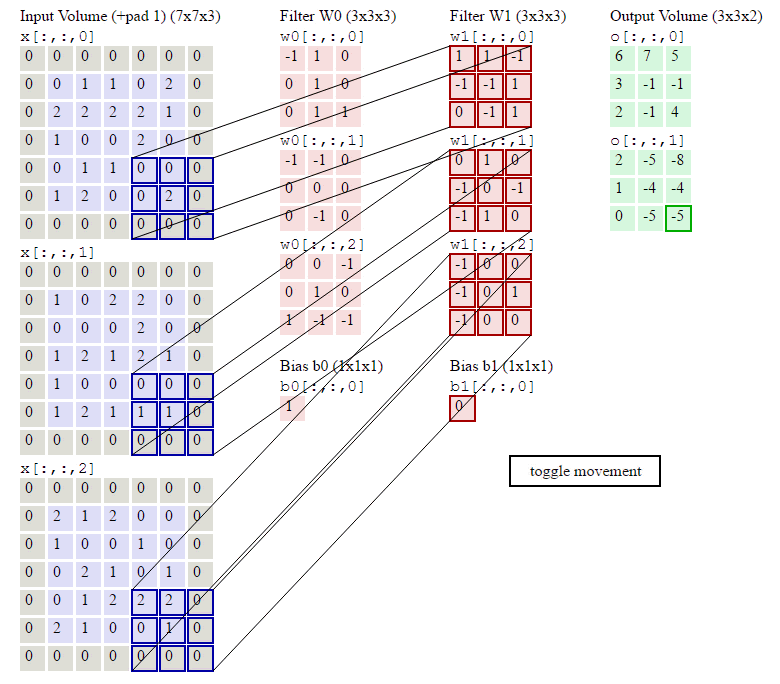
参数:输入Shape:\((7\times7\times3)\) 卷积核Shape:\(3\times3\times3\times2\) \(zero-padding=1 stride=2\)
输出Shape计算: \[ \begin{align} W_2 &= (W_1 - F + 2P)/S + 1\qquad(式2)\\ H_2 &= (H_1 - F + 2P)/S + 1\qquad(式3) \end{align} \]
卷积层
卷积层的作用是提取一个局部区域的特征,不同的卷积核相当于不同的特征提取器。上一节中描述的卷积层的神经元和全连接网络一样都是一维结构。既然卷积网络主要应用在图像处理上,而图像为两维结构,因此为了更充分地利用图像的局部信息,通常将神经元组织为三维结构的神经层,其大小为高度H×宽度W×深度C,有C个H ×W 大小的特征映射构成。 特征映射(feature map)为一幅图像(或其它特征映射)在经过卷积提取到的特征,每个特征映射可以作为一类抽取的图像特征。为了卷积网络的表示能力,可以在每一层使用多个不同的特征映射,以更好地表示图像的特征。
卷积层的关键参数:
- 卷积核大小(Kernel Size):定义了卷积操作的感受野。在二维卷积中,通常设置为3,即卷积核大小为3×3。
- 步幅(Stride):定义了卷积核遍历图像时的步幅大小。其默认值通常设置为1,也可将步幅设置为2后对图像进行下采样,这种方式与最大池化类似。
- 边界扩充(Padding):定义了网络层处理样本边界的方式。当卷积核大于1且不进行边界扩充,输出尺寸将相应缩小;当卷积核以标准方式进行边界扩充,则输出数据的空间尺寸将与输入相等。
- 输入与输出通道(Channels):构建卷积层时需定义输入通道I,并由此确定输出通道O。这样,可算出每个网络层的参数量为I×O×K,其中K为卷积核的参数个数。例,某个网络层有64个大小为3×3的卷积核,则对应K值为 3×3 =9。
卷积层特性:
局部连接:卷积计算的通俗理解就是卷积核在图像上做滑动卷积,每次滑动输出一个值,局部乘积求和。局部计算如:
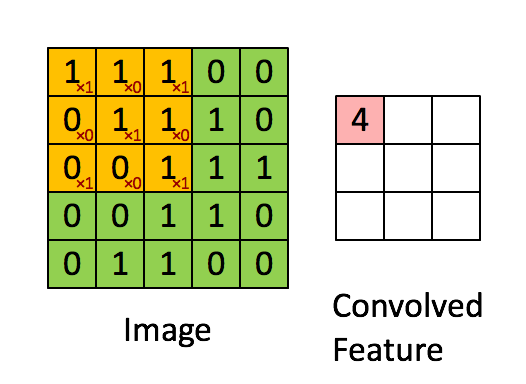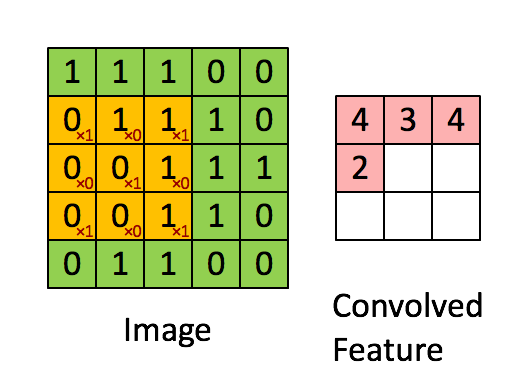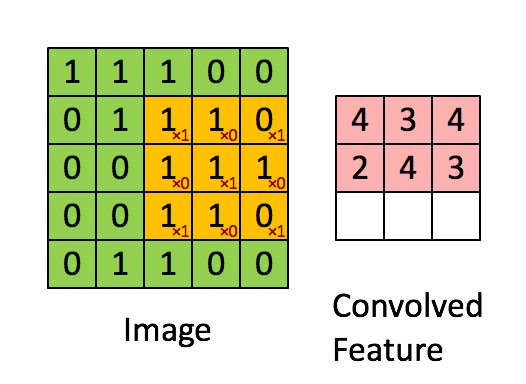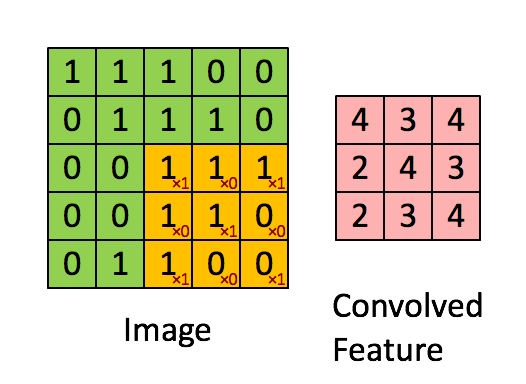
局部求和 权值共享:整张图像可以共用一个卷积核,对比全连接操作卷积不需要同时和每个像素点相乘求和(内积)。
池化(pooling)
池化也叫子采样(subsampling layer),其作用是进行特征选择,降低特征数量,并从而减少参数数量。
标准的卷积操作虽然可以显著减少网络中连接的数量,但特征映射组中的神经元个数并没有显著减少。如果后面接一个分类器,分类器的输入维数依然很高,很容易出现过拟合。为了解决这个问题,可以在卷积操作之后加上一个池化操作,从而降低特征维数,避免过拟合。(也可通过增加滑动卷积的步长Stride来达到降维效果)
池化操作虽然说有降维功能,同时也是存在信息损失的。
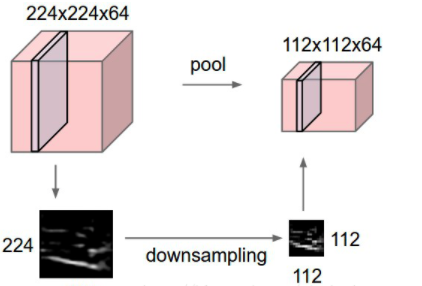
常见的池化方式
- 最大池化(max-pooling)
一般是在池化核对应区域内选取最大值来表征该区域。
- 平均池化(mean-pooling)
一般是取池化核对应区域内所有元素的均值来表征该区域。
- 全局池化(global pooling)
一般是对整个特征图进行最大池化或者平均池化。
- 重叠池化(overlapping-pooling)
相邻池化窗口之间会有重叠区域,此时kernel size>stride
卷积神经网络中的特殊卷积操作
\(1\times1\)卷积核
自从GoogLenet接手发扬光大以后,\(1\times1\)卷积广泛出现在新的卷积架构中如xception和小卷积网络中。\(1\times1\) 卷积核在单通道上就是给每个像素点同等乘以一个系数,多通道上其实现了通道间的信息流通。从全连接的角度解释即C通道特征图,和C个\(1\times1\)卷积核卷积输出1个新的特征图。同理,和KC个1x1的卷积核卷积输出K个特征图。注:全连接运算是元素级的,\(1\times1\)卷积是通道级的,对于HW * C的特征图全连接需要K * H * W * C,而11卷积仅需要KC个参数。图片来自知乎。 
\(1\times1\)卷积的作用
- 跨通道信息交互(channal 的变换)
- 升维(用最少的参数拓宽网络channal)
- 降维(减少参数)
深度可分离卷积(depthwise separable convolution)
深度可分离卷积在执行空间卷积,同时保持通道分离,然后进行深度卷积。 可分离卷积与标准的卷积相比,其在通道上先做了卷积然后在再用\(1\times1\)卷积进行通道融合。示意图:
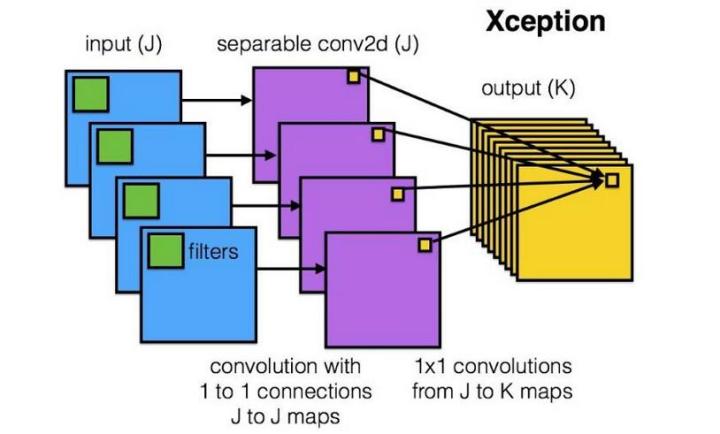
对比标准卷积过程:
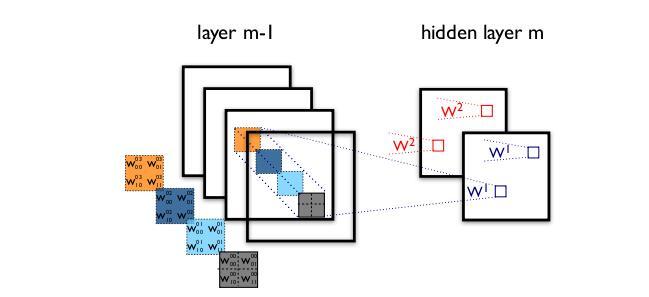
假设我们在16个输入通道和32个输出通道上有一个3x3卷积层。详细情况是,16个3x3内核遍历16个通道中的每一个,产生512(16x32)个特征映射。接下来,我们通过添加它们来合并每个输入通道中的1个特征图。由于我们可以做32次,我们得到了我们想要的32个输出通道。
针对这个例子应用深度可分离卷积,用1个3×3大小的卷积核遍历16通道的数据,得到了16个特征图谱。在融合操作之前,接着用32个1×1大小的卷积核遍历这16个特征图谱,进行相加融合。这个过程使用了16×3×3+16×32×1×1=656个参数,远少于上面的16×32×3×3=4608个参数。
这个例子就是深度可分离卷积的具体操作,其中上面的深度乘数(depth multiplier)设为1,这也是目前这类网络层的通用参数。这么做是为了对空间信息和深度信息进行去耦。从Xception模型的效果可以看出,这种方法是比较有效的。由于能够有效利用参数,因此深度可分离卷积也可以用于移动设备中。
空洞卷积(dilated convolution)
dilated convolution是针对图像语义分割问题中下采样会降低图像分辨率、丢失信息而提出的一种卷积思路。
空洞卷积的特点是在扩大感受野的同时不增加计算成本。示意图:
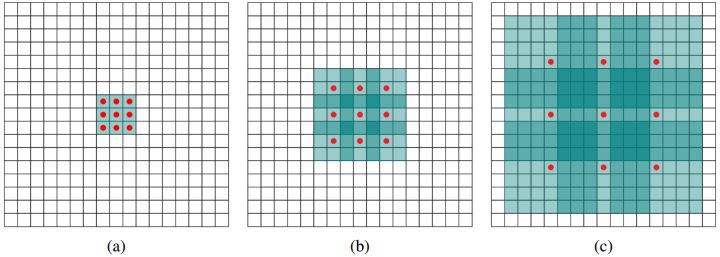
上图b可以理解为卷积核大小依然是3×3,但是每个卷积点之间有1个空洞,也就是在绿色7×7区域里面,只有9个红色点位置作了卷积处理,其余点权重为0。这样即使卷积核大小不变,但它看到的区域变得更大了 。
空洞卷积的动机:加pooling层,损失信息,降低精度;不加pooling层,感受野变小,模型学习不到全局信息
组卷积(Group convolution)
分组卷积(Group convolution) ,最早在AlexNet中出现,由于当时的硬件资源有限,训练AlexNet时卷积操作不能全部放在同一个GPU处理,因此作者把feature maps分给多个GPU分别进行处理,最后把多个GPU的结果进行融合(concatenate)。
下图分别是一个正常的、没有分组的卷积层结构和分组卷积结构的示意图:
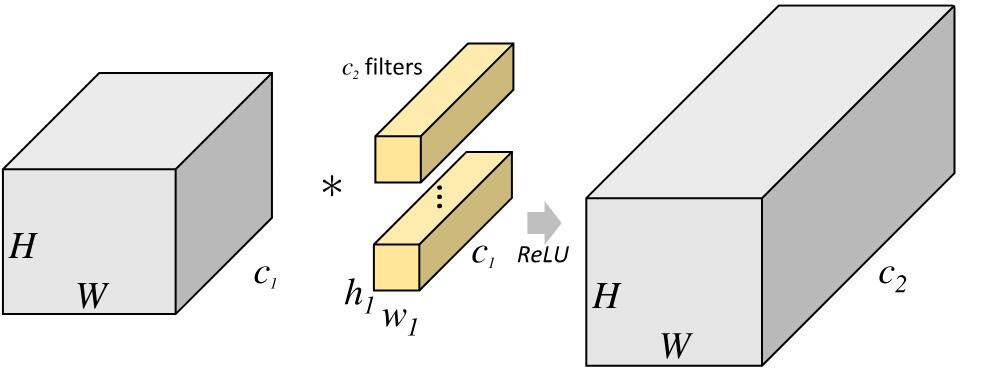
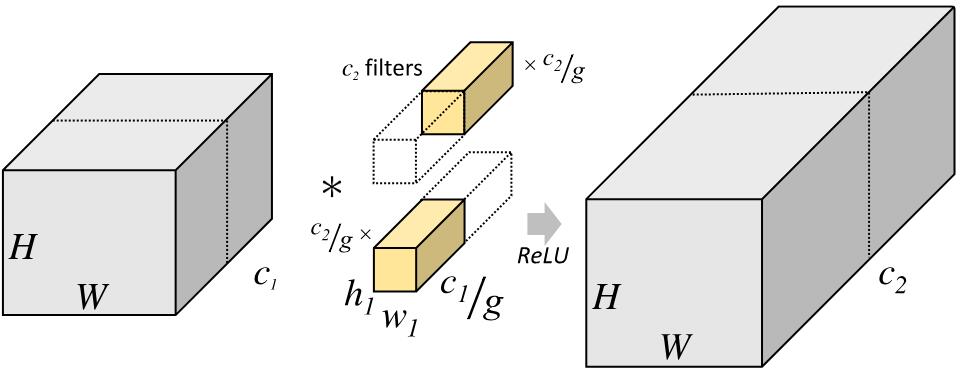
组卷积通过将卷积运算的输入限制在每个组内,模型的计算量取得了显著的下降。然而这样做也带来了明显的问题:在多层逐点卷积堆叠时,模型的信息流被分割在各个组内,组与组之间没有信息交换。这将可能影响到模型的表示能力和识别精度。 目前旷世科技提出的ShuffleNet引入通道重排来处理组和组之间的信息流通。
分组卷积操作实例:
从一个具体的例子来看,Group conv本身就极大地减少了参数。比如当输入通道为256,输出通道也为256,kernel size为3×3,不做Group conv参数为256×3×3×256。实施分组卷积时,若group为8,每个group的input channel和output channel均为32,参数为8×32×3×3×32,是原来的八分之一。而Group conv最后每一组输出的feature maps以concatenate的方式组合。 Alex认为group conv的方式能够增加 filter之间的对角相关性,而且能够减少训练参数,不容易过拟合,这类似于正则的效果。
转置卷积
反卷积是一种上采样操作,在图像分割和卷积自编码中应用较多。示意图:
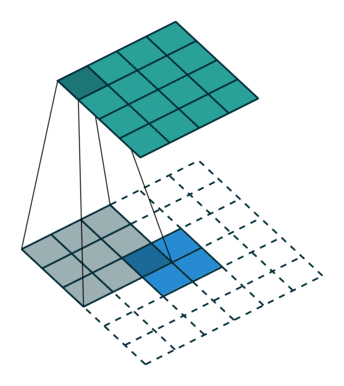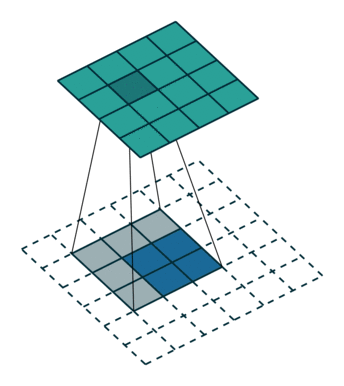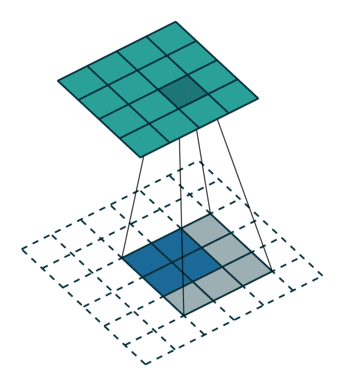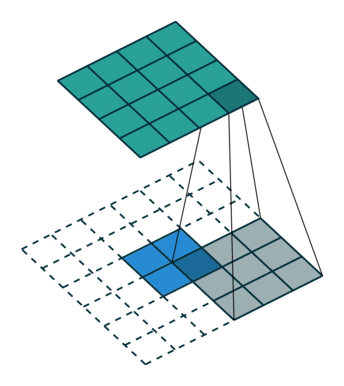
小结
本文简单的介绍了信号卷积的算法原理,引入二维离散卷积引导对卷积神经网络的卷积的理解。卷积是一种滤波操作,在卷积神经网络中有许多卷积变形结构,这些结构从维度控制,信息流通,模型参数大小控制,感受野等角度进行设计。在当前state of art卷积架构中多是融入了部分或者全部上述变形卷积。在设计新的模型时,可从设计目标出发采用上述结构优化,裁剪模型。
参考
邱锡鹏 ,《神经网络与深度学习》https://nndl.github.io/>
https://zhuanlan.zhihu.com/p/28749411
https://towardsdatascience.com/types-of-convolutions-in-deep-learning-717013397f4d
https://www.zhihu.com/question/54149221
https://www.cnblogs.com/ranjiewen/articles/8699268.html
https://blog.csdn.net/A_a_ron/article/details/79181108
